
A Quick Preview
Let us say we are faced with two hypothetical authentic (i.e. ṣaḥīḥ) hadiths from a respected collection such as Ṣaḥīḥ al-Bukhārī, with the following chain diagrams, and we are trying to decide which hadith is stronger and better attested. The first hadith below has four transmitters (the four on the right), all of whom narrate from a single transmitter, who narrates from a Companion:
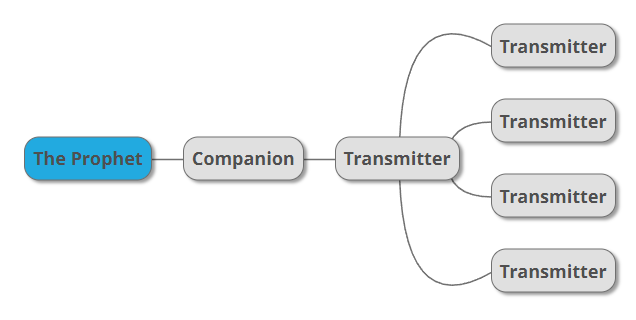
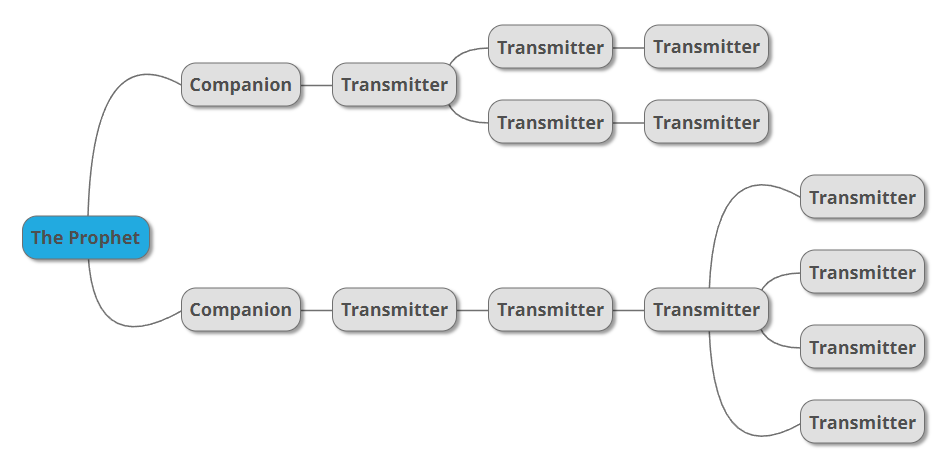
The second hadith has six transmitters, who transmit their hadiths from different chains going back to two Companions:
(For the sake of the example, we are assuming all of the transmitters are of the same quality, though the method can account for transmitters of varying qualities too).
When faced with comparing two such hadiths, it can be very difficult to decide which hadith is higher in quality when it comes to its isnād. The first hadith has “only” four chains, but the transmitters are only one generation removed from the Companions. Meanwhile, the second hadith has six chains, but the hadith’s transmitters are either two generations or three generations removed.
The second hadith goes back to two Companions, which seems to make it more trustworthy than the first hadith, which goes back to only one Companion. Yet the first hadith’s transmitters are only one generation removed from a Companion, compared to the second hadith’s two or three generation remove. How do we make sense of this situation so that we can decide which hadith is actually stronger?
The method described in this essay provides a mathematical method to precisely combine the strength of all of the chains of a particular hadith in order to assign it a single number that tells what strength all those differing chains amount to. The method does not introduce any new information to the science of hadith, it is merely a convenient “calculator” that hadith scholars (and other researchers) can use that can be replicated by others, making the act of judging hadiths a matter of measurement and replication, rather than a matter for hunches and appeals to the fame and authority of this or that person.
As it happens, in the above example the first hadith is somewhat stronger, having a score of 35%, compared with the second hadith’s score of 30%. As will be shown, relatively few hadiths, including ṣaḥīḥ ones, reach above 30% in their scores, so both of the hadiths are reasonably strong and well worth using in legal judgments.
Introduction
The study of hadith has been by and large restricted to hadith scholars. In this essay I present a fundamentally new approach to the study of hadith that combines the disciplines of traditional hadith criticism with uṣul al-fiqh (legal theory). For over a millennium, scholars of legal theory have discussed what makes certain hadiths mutawātir, or true beyond doubt, but these discussions have unfortunately been almost entirely ignored by hadith scholars. By combining legal theory with hadith criticism, we gain a powerful new empirical tool for judging the authenticity of hadiths that enables fiqh scholars to tap the vast resources of the science of hadith while implementing the long-neglected field of legal theory in the way hadiths are handled.
Counting the number of chains that a hadith possesses has been a traditional method of determining the strength of one hadith compared to another. Another method has been to determine the length of a chain. Hadiths with shorter chains were highly prized due to their higher authenticity. This method integrates both of these concepts: Hadiths with more chains and shorter chains receive higher percentage rankings than hadiths with fewer chains or shorter chains.
From binary to analog
It is rarely mentioned in scholarly circles and among the rest of the Muslim community that the categories that hadiths are placed into by hadith scholars, such as ṣaḥīḥ, are artificial, made-up categories. Some ṣaḥīḥ hadiths are vastly superior in their authenticity compared to other ṣaḥīḥ hadiths, and hadith scholars are well aware of this.
It was natural and convenient for hadith scholars of the early and classical periods to view hadiths as being either ṣaḥīḥ or not-ṣaḥīḥ (ḥasan, ḍaʿīf, etc.). This is what I call binary thinking. It divides the world of hadith into two parts, one of which, ṣaḥīḥ, is assumed to be practically perfectly reliable despite the awareness that no two ṣaḥīḥ hadiths are ever equally reliable. It’s similar to dividing one’s friends and acquaintances into two categories, “trustworthy” and “untrustworthy”, despite the fact that we know the real world is much more complicated than that and that people, in reality, are on a spectrum of trustworthiness from most trustworthy to least trustworthy.
The essential innovation that my verification method introduces is that it supersedes the artificial, binary thinking of traditional hadith science by introducing an analog method of categorizing hadiths, suggested to me not by hadith scholars but by scholars of legal theory in their discussions of the reliability of hadiths, that better represents reality. In the traditional method a hadith can either be ṣaḥīḥ or not-ṣaḥīḥ, while in my method a hadith can be 20% likely to be authentic, or 30%, or 90%. The method has room for representing all the various shades of authenticity that are hidden to ordinary Muslims when they read that a particular hadith is authentic.
This method helps free the great treasures of the science of hadith criticism that have so far been locked away in hadith collections and the works of hadith transmitter criticism (ʿilm al-rijāl) so that every Muslim can benefit from them by having that knowledge translated into an easy-to-understand mathematical ranking system.
Hadith and probability theory
Islam’s hadith literature (reports about the actions and sayings of the Prophet PBUH) is one of the most problematic aspects of the religion due to the issues concerning the reliability of transmitters. How do we know if a report going back six or seven generations to the Prophet PBUH truly and accurately reports what the Prophet PBUH said or did?
So far the science of hadith has largely limited itself to verifying the authenticity of hadiths by verifying the trustworthiness of each person in a hadith’s chain of narrators. If all the transmitters are trustworthy, the assumption is that the hadith is ṣaḥīḥ (“authentic” or “sound”) unless the hadith reports things that are clearly false or contradictory to other hadith narrations. The problem is that a hadith scholar’s own beliefs and biases can strongly affect whether they consider a strange and rare hadith to be authentic or not. A good example is the following hadith in Imām al-Bukhārīʾs collection:
Narrated Abu 'Amir or Abu Malik Al-Ash'ari that he heard the Prophet (ﷺ) saying, "From among my followers there will be some people who will consider illegal sexual intercourse, khazz (a type of clothing), the wearing of silk, the drinking of alcoholic drinks and the use of musical instruments, as lawful. And there will be some people who will stay near the side of a mountain and in the evening their shepherd will come to them with their sheep and ask them for something, but they will say to him, 'Return to us tomorrow.' Allah will destroy them during the night and will let the mountain fall on them, and He will transform the rest of them into monkeys and pigs and they will remain so till the Day of Resurrection."
(Ṣaḥīḥ al-Bukhārī 5590)
A non-scholar who reads this hadith will be greatly troubled by the implication that the use of musical instruments is a characteristic of misguided and impious Muslims. And since the hadith is authentic and present in Ṣaḥīḥ al-Bukhārī, they will face the difficult choice of either believing musical instruments (and hence all music) to be forbidden in Islam, or ignoring the hadith and going with the commonsense and widespread Muslim belief that music is permissible in Islam.
By introducing probability theory into the science of hadith, we gain an extremely powerful tool that enables us to judge just how seriously we should take any particular hadith. This is especially useful in the case of hadiths that seem to be contradicted by other hadiths. For example on the issue of musical instruments we have the following hadith:
Narrated Aisha:
Abu Bakr came to my house while two small Ansari girls were singing beside me the stories of the Ansar concerning the Day of Buath. And they were not singers. Abu Bakr said protestingly, "Musical instruments of Satan in the house of Allah's Messenger (ﷺ) !" It happened on the `Id day and Allah's Messenger (ﷺ) said, "O Abu Bakr! There is an `Id for every nation and this is our `Id."
Sahih al-Bukhari 952
An authentic version of this hadith (Sahih Muslim 892 b) tells us that the girls were using the instrument daff (“tambourine”). So here we have the Prophet PBUH approving of the use of musical instruments in his own home, yet the other hadith implies that musical instruments are wicked and unlawful.
Probabilistic hadith criticism helps solve the dilemma of having to choose between two hadiths that are both judged authentic by hadith scholars by telling us which one is stronger.
As it happens, the hadith mentioning the Prophet’s approval of musical instruments is far more “authentic” and believable than the hadith in which he disapproves of them.
In this essay I will use these hadiths on music as an illustration of the probabilistic hadith verification method.
Gathering the hadiths approving of music
The first step in hadith verification is to gather all existing versions of a hadith and their chains and to draw a diagram representing all of its transmitters. Below is a diagram of the version of the “two singing girls” hadiths found in Sahih al-Bukhari:
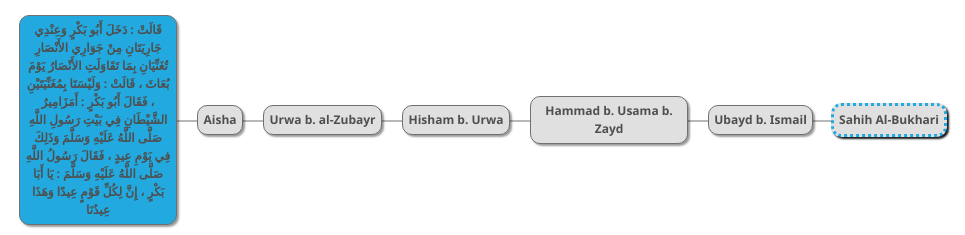
The blue box is the hadith, and the gray boxes are its transmitters. The first transmitter is Aisha, may God be pleased with her, wife of the Prophet PBUH. The second transmitter is Urwa b. al-Zubayr, her nephew. The third transmitter is Urwa’s son Hisham. The the fourth transmitter is the highly respected hadith scholar Hammad b. Usama b. Zayd. The fifth transmitter is Ubayd b. Ismail, a respected hadith transmitter. This transmitter gave the hadith to Imam al-Bukhari who recorded it.
The second version of the hadith is also in Sahih al-Bukhari:
Narrated Aisha:
That once Abu Bakr came to her on the day of `Id-ul-Fitr or `Id ul Adha while the Prophet (ﷺ) was with her and there were two girl singers with her, singing songs of the Ansar about the day of Buath. Abu Bakr said twice. "Musical instrument of Satan!" But the Prophet (ﷺ) said, "Leave them Abu Bakr, for every nation has an `Id (i.e. festival) and this day is our `Id."
Sahih al-Bukhari 3931
Below is a diagram of this hadith’s chain:
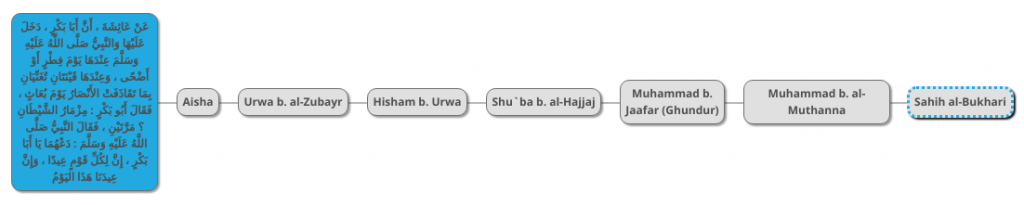
You may note that the first three transmitters are the same as those of the previous hadith. So we can join their diagrams into one as follows:

Next is the chain found in Sahih Muslim 892 a:
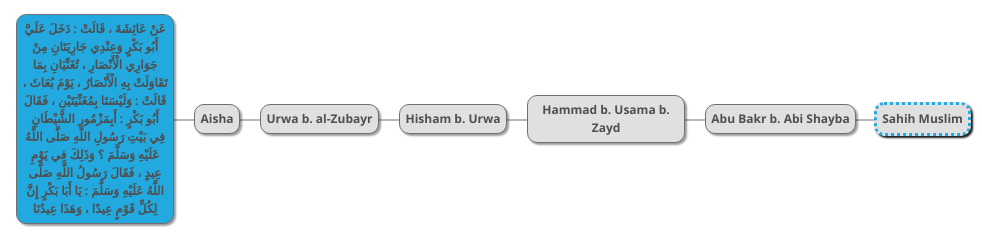
This chain is exactly the same as the al-Bukhari’s first chain except for the last transmitter. We can therefore join it with the rest as follows:
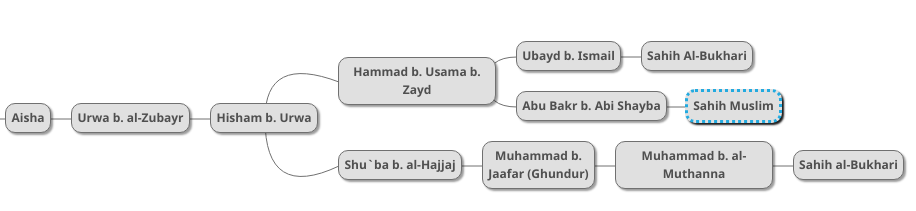
We now therefore have three chains going back to the same hadith. Imam Muslim mentions two additional chains which we add to the diagram as follows:

We now move on to other collections that mention the same hadith. The first one is a version mentioned in Abu Uwaana’s Mustakhraj, which we add to the diagram as follows:
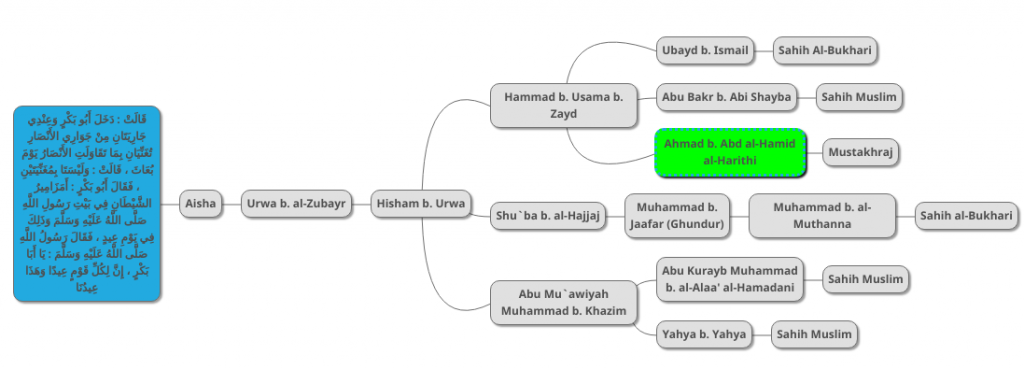
I have indicated the new chain in green. After further research, I was able to discover a further chain in Sahih al-Bukhari as indicated below:
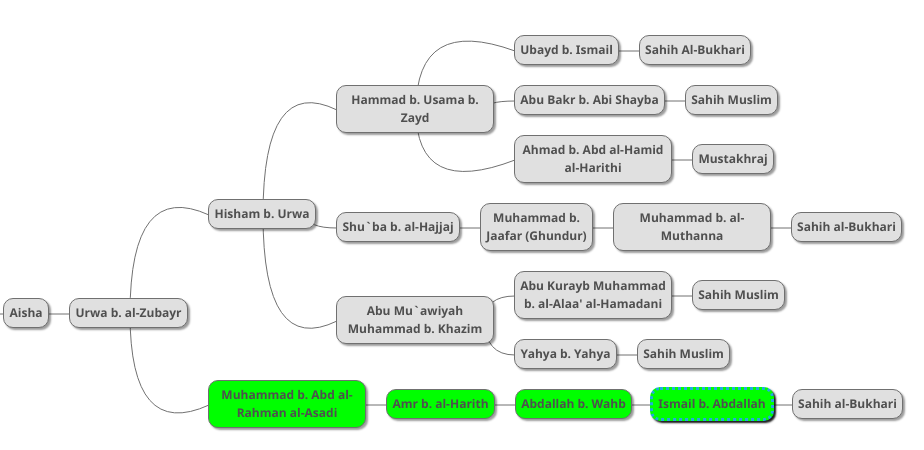
Al-Bukhari mentions an alternative version of this new chain as indicated below:
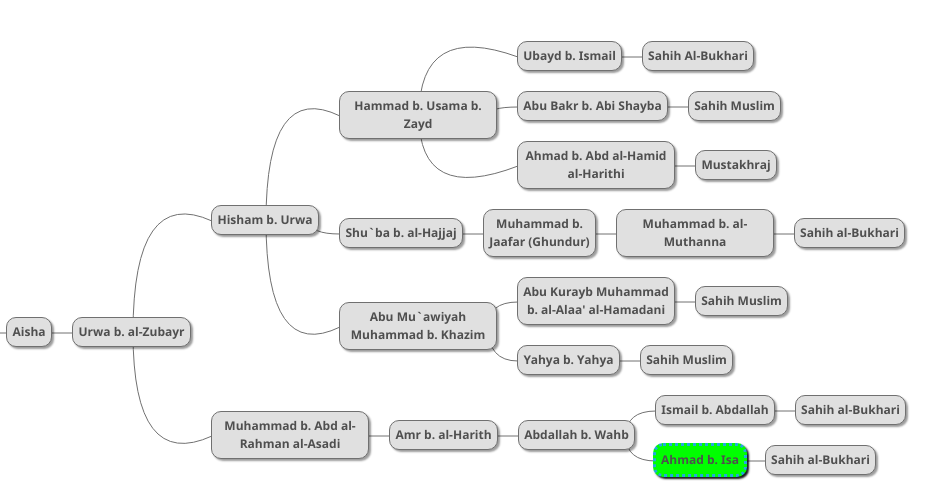
The scholar Abu Uwana adds two of his own supporting chains to this version as follows:

We now have a fairly complete picture of all of the different chains of this hadith.
Adding the probabilities
To understand this section, some previous knowledge of probability theory will likely be required.
In order to start, we have to agree on an important assumption. How trustworthy is a single transmitter? This is a matter of intuition. After trying out various probabilities, I have settled on the value of 60%. This means that each trustworthy transmitter in a chain has a 60% chance of truthfully and correctly transmitting the hadith they transmit. This may seem low, but it actually works very well to represent the issues inherent in hadith transmitter verification.
This 60% is not a judgment on the transmitter’s character. It is a judgment on this specific piece of information in this specific place in the chain. It does not mean that a transmitter is 60% likely to be trustworthy. Rather, it is based on the uṣūl al-fiqh (Islamic legal theory) discussions on the number of witnesses needed for a certain piece of information to be considered mutawātir or true beyond doubt (see Wael B. Hallaq in Islamic Law and Jurisprudence: Studies in Honor of Farhat J. Ziadeh). It is general knowledge among scholars of legal theory that a single witness, no matter how trustworthy, can never impart certain knowledge. This is why Islamic law requires multiple witnesses in various legal cases. This requirement for multiple witnesses is not a judgment on the character of individual witnesses. It is a guarantee against various forms of error and uncertainty. According to the 60% assumption, four trustworthy witnesses mentioning the same piece of information side-by-side have a 97.44% chance of imparting it truthfully and correctly, while eight witnesses have a 99.93% chance, making a piece of information practically mutawātir, or widely-transmitted.
The 60% assumption takes into account the concept of signal decay. While a trustworthy witness who heard a piece of information today may have a 100% chance of imparting it correctly today, hadiths are transmitted between witnesses who may have held onto the information for decades. A hadith with four transmitters in its chain may in fact represent information passed down over four generations. There is an inherent signal decay in this multi-generational process, and the 60% assumption helps simulate this decay by requiring multiple transmitters at each point of the chain to maintain signal integrity.
According to probability theory, if you have a witness with 60% probability of truthfulness saying something, and then a second witness also with 60% probability of truthfulness comes along and says the same thing, the probability of both of them saying the truth increases, since we have two witnesses saying the same thing. We calculate this increase by multiplying the falsehood probabilities of the two persons as follows:
Person 1: 60% chance of truth = 40% chance of falsehood
Person 2: 60% chance of truth = 40% chance of falsehood
The chance of falsehood for both = 40% * 40% = 16%
The chance of truth of both = 100% - the chance of falsehood = 100% - 16% = 84%
Below is a diagram of an imaginary chain that represents these facts:
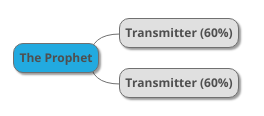
We have two people each of whom say that the Prophet PBUH said something. Each of them has a 60% probability of truthfulness and accuracy, but the two of them together have a 84% probability of truthfulness and accuracy, so the above imaginary hadith has an 84% chance of truthfulness and accuracy.
As we add more transmitters, the probability continually goes up:

Now we have four supporting witnesses, so their probability of truthfulness can be calculated as follows:
Falsehood probabilities: 40% * 40% * 40% * 40% = 2.56%
Truth probability: 100% - 2.56% = 97.44%
What this means is that if you have four Companions transmit the same hadith from the Prophet PBUH, the chance of the hadith being truly and correctly transmitted is 97.44%, which is a very high chance.
In probability theory 1 represents 100% and 0 represents 0. So another way of doing the above calculation is as follows:
0.4 * 0.4 * 0.4 * 0.4 = 0.0256
1 - 0.0256 = 0.9744
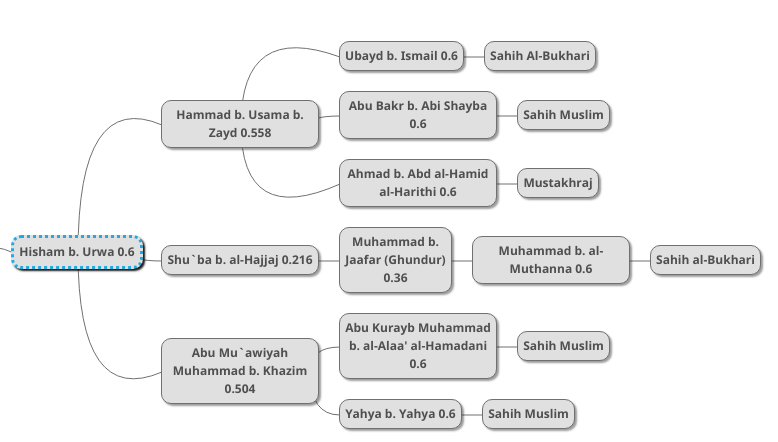
The benefits of the 60% assumption will become clear as we go through the verification process of the chains we gathered earlier. We will first deal with the top part of the diagram, which is as follows:

First, we will fill in the original 60% assumption by writing 0.6 in each bubble:

We do not add the 0.6 to the bubbles on the far right because those are written books, so they virtually have a 100% chance of reliability. What concerns us are unwritten, oral transmissions. The first step is to combine the three middle transmitters’ probabilities vertically, as follows:
Falsehood chances: (1-0.6) * (1-0.6) * (1-0.6) = 0.064
Truth chance: 1 - 0.064 = 0.936
Above, each of the three transmitters has a 100% – 60%, or 40% likelihood of falsely transmitting the hadith. But in order to get the probability of all of them falsely transmitting the hadith at the same time, we have to multiply these chances together: 40% * 40% * 40% = 6.4%. So the chance of all of them having falsely transmitted the hadith is only 6.4%, meaning that there is a 93.6% chance of them having truly and accurately transmitted this hadith.
We will call this “vertical combination”. We vertically combine all of the probabilities of the truthfulness and accuracy of the transmitters to get a single number, in this case 93.6%, which represents the authenticity of all them combined together.
We next have to do a horizontal combination. All three transmitters transmit the hadith from Hammad b. Usama, who also has a 0.6 (60%) chance of authenticity.
In the case of horizontal combination, rather than multiplying falsehood probabilities, we multiply truth probabilities. The reason is that as information passes down through a chain of transmitters each of whom have a 60% chance of authenticity, the chance of the information being correctly passed down decreases. There is more chance for error and fabrication. If you hear a Companion say that the Prophet PBUH said something, that is far more trustworthy than another person saying they heard their father say that their grandfather said that a Companion said that the Prophet PBUH said that.
So we multiply 0.93 by 0.6 to get 0.558, which means 55.8%. We now update the bubble for Hammad b. Usama to represent this new probability:

Hammad b. Usama’s probability went down from 0.6 to 0.558 because we did not hear the hadith directly from him, but from three people who claim to have heard him. Since those three people have a combined probability of 93% truthfulness and accuracy (rather than 100%), this slightly decreases the probability of the truthfulness and accuracy of the information we get from Hammad b. Usama.
We now move on to al-Bukhari’s second chain, which is as follows:

Using horizontal combination:
0.6 * 0.6 * 0.6 = 0.216
So this second chain has only a 21.6% probability of truthfulness and accuracy. The reason is that we do not have any supporting transmitters. We only have Muhammad b. al-Muthanna’s word for it that Muhammad b. Jaafar said that, and we only have Muhammad b. Jaafar’s word for it that Shu`ba said that. The deeper a chain goes back in time, the lower its probability of authenticity and accuracy becomes.
We next deal with two chains from Sahih Muslim:
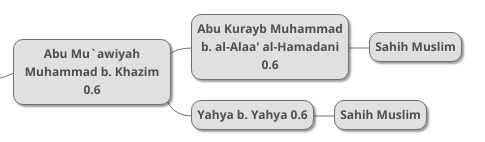
Using vertical combination for the middle transmitters, we get a probability of 0.84 or 84%. Multiplying that by 0.6, we get 0.504, meaning that Abu Mu`awiyah has a 50.4% probability of authenticity.
Next we have the more interesting task of combining all the chains we examined above. We have to vertically combine the probabilities of Hammad (0.558), Shu`ba (0.216) and Abu Mu`awiyah (0.504):
Falsehood probabilities: (1-0.558) * (1-0.216) * (1-0.504) = 0.171877888
Truth probability: 1 - 0.171877888 = 0.828122112
So the probability of the truth of the information coming from these three transmitters is 82.8%.
Now we horizontally combine this with Hisham b. Urwa’s 0.6 probability, resulting in 0.496873267
We repeat these same steps for the remaining chains, as follows:
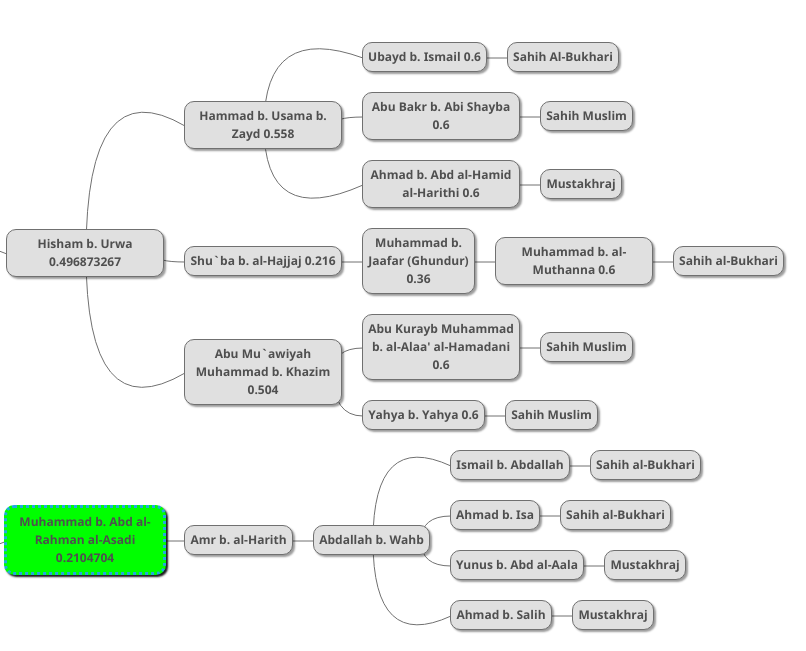
And by vertically combining the left-most probabilities (Hisham b. Urwa’s 49.68% and Muhammad b. Abd al-Rahman’s 21.04%), we get 0.602766552, so the information has a 60.27% probability of authenticity at this stage.
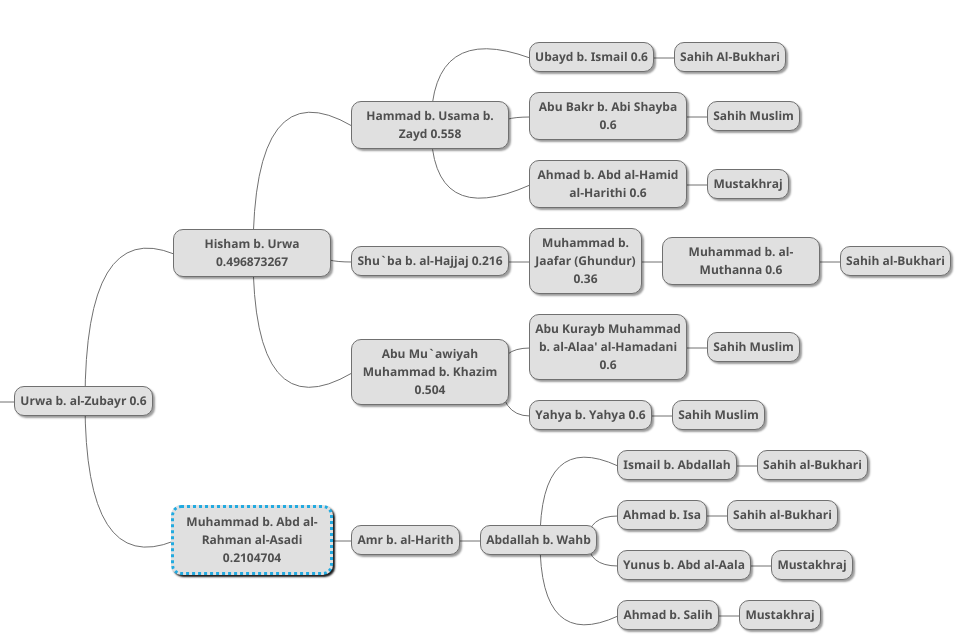
We next multiply this 0.602766552 by Urwa b. al-Zubayr’s 0.6 (horizontal combination), resulting in 0.361659931.
In the final step, we multiply this result by Aisha’s 0.6:
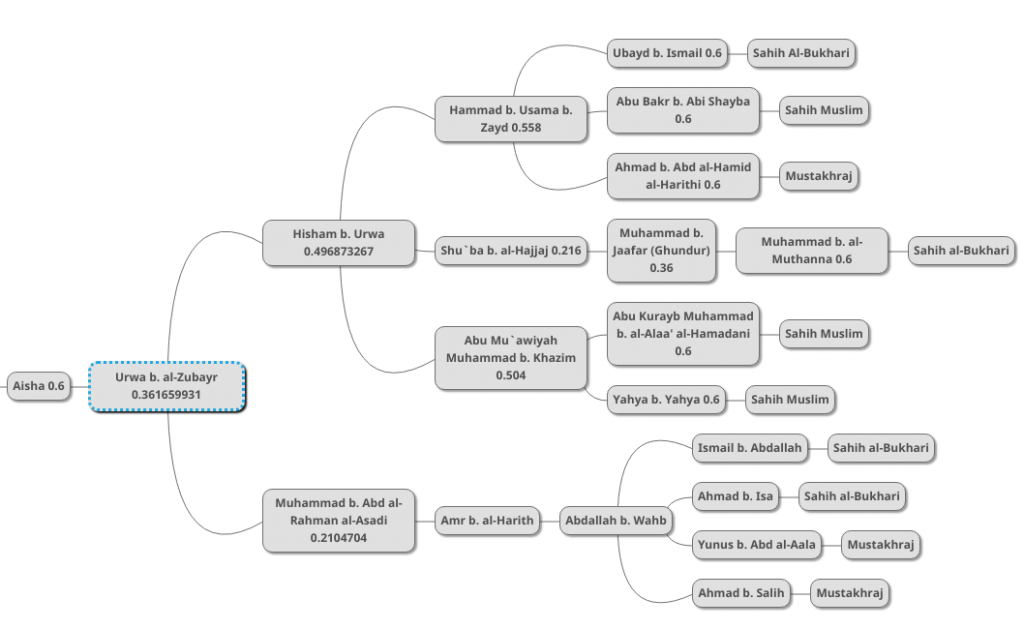
The result is 0.216995959. This means that the hadith with all of its chains has a 21.69% chance of authenticity and accuracy. This seems very low, but it is natural for a hadith that comes from a single Companion, through a single transmitter.
In my methodology, a hadith that reaches 20% or higher is ḥasan, a hadith that reaches 30% or higher is ṣaḥīḥ, a hadith that reaches 60% or higher is ṣaḥīḥ al-ṣaḥīḥ (a degree above ṣaḥīḥ), and a hadith that reaches 85% or higher is mutawātir (“widely transmitted”, a degree above ṣaḥīḥ al-ṣaḥīḥ).
Note that the method can easily be tweaked so that ṣaḥīḥ would start at 50% instead of 30%.. Instead of giving a transmitter in a chain a probability of 60%, we can give them a probability of 80%, which would increase the results arrived it. Note that it makes no difference what assumption we choose, as I have chosen 60%, for an individual transmitter, because the end result is always relative to other hadiths. Regardless of what assumption we choose, it is the case that a hadith with a stronger chain will receive a higher rank than a hadith with a weaker chain.
Different scholars may prefer different probabilities for what they consider ḥasan or higher. Personally these are the numbers I have settled on that my heart is comfortable with and accepts.
The hadith disapproving of music
We now move on to Ṣaḥīḥ al-Bukhārī 5590, the hadith that says misguided Muslims will approve of musical instruments. Below is a diagram of the hadith’s chain:

The hadith comes from a single chain that does not branch out, meaning it is an extremely questionable chain, which I call a “precarious” chain. To calculate its probability of authenticity, we horizontally combine all the 0.6 probabilities as follows:
Probability of truth = 0.6 * 0.6 * 0.6 *0.6 *0.6 *0.6 = 0.046656
This hadith therefore has a 4.66% chance of authenticity, which is extremely low. In my thinking a hadith between 10% and 20% is munkar (strange and likely to be false), while a hadith below 10% is ḍaʿīf (“weak”, i.e. almost certainly false). As discussed in another article, there is another reason to consider this hadith questionable: it says misguided Muslims will consider khazz (a type of clothing) lawful. But we know 20 Companions of the Prophet PBUH wore this type of clothing, so this makes the hadith even more dubious.
The verdict
The hadith in which the Prophet PBUH says misguided Muslims will consider musical instruments lawful has only a 4.66% chance of authenticity, while the hadith in which the Prophet PBUH approves of musical instruments has a 21.69% chance of authenticity. Thus the hadith in which the Prophet PBUH approves of musical instruments is 4.6 times stronger than the hadith in which he disapproves of them (21.69 ÷ 4.66 = 4.65).
Based on this, we can confidently say that the evidence in support of the lawfulness of musical instruments is far stronger. Therefore approval of musical instruments is a vastly better representation of the Prophet’s sunna (tradition) than disapproval of them.
Defending the assumptions
The assumption that each transmitter has a 60% chance of accurately and truthfully transmitting the information needs to be defended. This assumption makes most ṣaḥīḥ narrations get an authenticity around 30%. If we treat these numbers empirically, it would mean that most authentic narrations are more likely to be false than true. For this reason I have chosen to treat all hadiths that reach 30% or higher as ṣaḥīḥ / authentic despite the fact that empirically they fall beneath the truth threshold of 50%.
My reasoning is that by choosing these assumptions, we create an interface between the empirical research world and the classical hadith studies world. A non-Muslim scholar may choose the 30% verdict on an authentic narration as a cause for skepticism, while a Muslim scholar can continue to make use of probability theory while adopting the traditional view of considering individual, low-truth-probability hadiths as authentic.
Another reason for the 60% assumption is that it gives us a very wide range of results. Some hadiths will reach close to 100%, many others will hover between 50% and 20%. This allows for representing a scholar’s empirical intuitions about these transmitted pieces of information, while also allowing them to remain in the classical hadith criticism world if they wish by choosing lower numbers, such as 30%, to represent full authenticity.
The study of Islam works on the basis of the autonomous consensus of the researchers, a concept I have defended elsewhere.1 Therefore introducing probability theory into hadith criticism will require the involvement of many researchers until a consensus emerges on the best assumptions to be chosen. Therefore my assumptions in this article are merely preliminary suggestions intended to illustrate what a probabilistic study of hadith would look like.
Conclusion
Combining probability theory and hadith criticism can greatly help in resolving issues surrounding contradictory hadith narrations by making it clear which hadiths are superior to which ones. It would be extremely helpful if we could build a new hadith collection that shows the probability of authenticity of each hadith rather than merely saying whether it is authentic or not. But such a work would require many years of work.
There is also the issue of sub-par transmitters. While I have chosen a probability 60% for reliable transmitters, for transmitters who are mudallis, non-qawī, non-ḥujja, or considered weak by some scholars and not others, lower probabilities will have to be used where necessary.
There are also different levels of weak transmitters. Some are considered weak for ideological reasons (because they held beliefs that hadith scholars considered unacceptable), while others are considered weak because they were caught lying or fabricating hadiths. Different probabilities will have to be used for different levels of weakness.
Further applications of the probabilistic method
See the articles on the Probabilistic Hadith Verification page for many studies by me in which I use the methodology developed in this article to verify hadiths on various important issues.